[Complex numbers] are essential to quantum physics, electromagnetism, and many more fields. They are naturally suited to describe anything that turns, waves, ripples, combines or interferes, with itself or with others. […] Whenever we’re describing wavelike phenomena, whether it’s sound, electricity or subatomic particles, we’re also interested in how the wave evolves and changes. Complex operations are eminently suited for this, because they naturally take place on circles. Numbers that oppose can cancel out, numbers in the same direction will amplify each other, just like two waves do when they meet. (http://acko.net/blog/how-to-fold-a-julia-fractal/)
A complex number \(z\) can be defined as
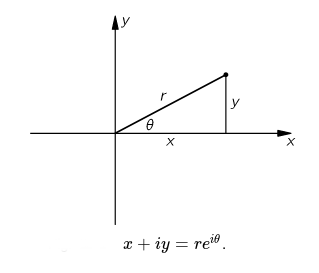
- \(z=x+yi\) with a real part \(x\) and an imaginary part \(y\)
- \(z=re^{i\theta}\) with magnitude \(r\) (its distance to the origin) and phase angle \(\theta\)
Where \(i^2=-1\) . And thus:
\((x,y)\) is a Cartesian coordinate.
- \(x = r\,\text{cos}(\theta)\)
- \(y = r\,\text{sin}(\theta)\)
\((r,\theta)\) is a polar coordinate, with \(r\) the modulus and \(\theta\) the argument.
- \(r = |z| = \sqrt{x^2 + y^2}\)
- \(\theta = \text{atan}2(y,x)\)
It holds that \(|z^n| = |z|^n\) and \(\text{arg}(z)^n = n\,\text{arg}(z)\) . And note that the phase angle comes from:
\(\quad\text{tan}(\theta) = \cfrac{\text{sin}(\theta)}{\text{cos}(\theta)} = \cfrac{y}{x}\)Figure from the Feynman lectures on algebra:
Arithmetic operations
Code: complex.exs
While addition is straight-forward in Cartesian form, most operations are much more intuitive in polar form, as they constitute transformations in the Cartesian plane.
Addition
- \((x_1+y_1i) + (x_2+y_2i) = (x_1+x_2) + (y_1+y_2)i\)
Multiplication
- \(\quad(x_1+y_1i)(x_2+y_2i) = (x_1x_2 - y_1y_2) + (x_1y_2 + x_2y_1)\)
- \((r_1e^{i\theta_1})(r_2e^{i\theta_2}) = r_1r_2e^{i(\theta_1+\theta_2)}\)
n-th power
- \((re^{i\theta})^n = r^n e^{in\theta}\)
Division
- \(\quad\cfrac{x_1+y_1i}{x_2+y_2i} = \cfrac{x_1x_2 + y_1y_2}{x_2^2+y_2^2} + \cfrac{x_2y_1 - x_1y_2}{x_2^2+y_2^2}i\)
- \(\cfrac{r_1e^{i\theta_1}}{r_2e^{i\theta_2}} = \cfrac{r_1}{r_2} e^{i(\theta_1-\theta_2)}\)
Reciprocal
- \(\cfrac{1}{x+yi} = \cfrac{x-yi}{x^2+y^2}\)
- \(\cfrac{1}{re^{i\theta}} = \cfrac{1}{r}e^{-i\theta}\)
Complex conjugate
Taking the complex conjugate corresponds to negating the imaginary component:
$$\overline{x+yi} = x-yi$$ $$\overline{re^{i\theta}} = re^{-i\theta}$$
This is equivalent to reflecting the complex number across the real axis.
Multiplying a complex number by its conjugate, we get a real number (the square of its distance to the origin):
$$z\,\overline{z} = x^2+y^2 = |z|^2$$Euler’s formula
What is the exponential function \(e^{x+yi}\) ? Using the exponential law yields \(e^{x+yi} = e^{x}e^{yi}\) , so the question boils down to: What is \(e^{yi}\) ? Euler defined this with what is now known as Euler’s formula: $$e^{iy} = \text{cos}(y)+i\,\text{sin}(y)$$ (For the complex conjugate we have \(e^{-iy} = \text{cos}(y)-i\,\text{sin}(y)\) .)
Because this is how everything else works out (like \(\frac{d}{dt}e^{it}=ie^{it}\) and exponential laws, including \(e^{0+0i}=1\) ). So we have: $$e^{x+yi} = e^x(\text{cos}(y)+i\,\text{sin}(y))$$ And: \(|e^{iy}|=1\) .
For any complex numbers \(z,w\) , we get:
\(e^{z+w}=e^ze^w\) \((e^z)^n=e^{n\,z}\) (in particular \((e^z)^{-1}=e^{-z}\) )
Solving real problems in the complex domain
Every algebraic equation can be solved in the complex domain.
Some problems are easier to solve in the complex domain than in the real domain, even if they have a real solution. For example: The integral of the real part of a complex number is the real part of the integral of the complex number (which might be much easier to integrate than the real one).