Electromagnetic and weak force
Electromagnetism is the interaction between objects due to their charge. This comprises attraction and repulsion between charged particles.
The weak nuclear force is the interaction between subatomic particles with “color”.
Strong nuclear force
The strong nuclear force is the interaction between subatomic particles with “flavor”.

Gravitational force
Gravity is the interaction between objects due to their mass. It is a relatively weak force (compared to others), but operates over long distances.
$$F = \frac{GMm}{r^2}$$ Where:
- \(G\) is the gravitational constant
- \(M\) and \(m\) are the masses of the two bodies
\(GM\) is the standard gravitational parameter \(\mu\) of a celestial body.
Consider a spacecraft of mass \(m\) in the gravitational field of a much larger mass \(M\) . That is, \(m << M\) and the center of mass of the two bodies is practically at the center of the large mass.
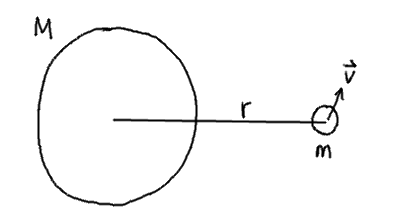
The velocity of an object in circular orbit is \(v^2=\cfrac{GM}{r}\) , so the farther away the object is, the slower it is. Note that \(m\) does not matter, as any object at the same distance \(r\) moves at the same velocity.
Sphere of influence and escape velocity
When leaving a body’s sphere of influence, you need to reach the required escape velocity, which depends on your distance \(r\) from the body’s center: $$v_\text{escape} = \sqrt{\frac{2GM}{r}}$$
For the Earth, this amounts to ~ 11.2 km/s from the surface and less from higher altitudes.
The hyperbolic excess velocity is the residual velocity you have left when you reach the boundary of the body’s sphere of influence. It will be constant until infinity (or at least would be if there were no other bodies exerting any force on you). So if you start with just the escape velocity, your hyperbolic excess velocity will be 0; anything you add to the escape velocity will be your hyperbolic excess velocity.
Energy
The total energy in a gravitational field is the sum of the kinetic energy and the potential energy. In a conservative force field (e.g. a gravitational force field without dissipative forces), mechanical energy is preserved.
Potential energy: $$E_{\text{pot}} = - G M \frac{m}{r}$$
Kinetic energy: $$E_{\text{kin}} = \frac{1}{2}\,m\,v^2$$