Eine \(m\times n\) -Matrix über einem Körper \(\mathbb{K}\) ist eine Anordnung von Elementen von \(\mathbb{K}\) nach folgendem Schema (mit \(m\) Zeilen und \(n\) Spalten): $$\begin{pmatrix} a_{11} & \ldots & a_{1n} \\ \vdots & \cdots & \vdots \\ a_{m1} & \ldots & a_{mn} \end{pmatrix}$$

Die Menge aller solcher Matrizen wird mit \(M_{mn}(\mathbb{K})\) bezeichnet.

Eine Matrix kann gesehen werden als \(n\) Vektoren (die Spalten) in einem \(m\) -dimensionalen Raum.

Matrizen können auch über einem kommutativen Ring statt einem Körper definiert werden. Matrizen über kommutativen Ringen können aber nicht notwendigerweise in eine Normalform überführt werden.

Matrizenrechnung

Addition und Skalarmultiplikation passieren elementweise.

Die Matrizenmultiplikation ist eine Verknüpfung \(M_{mk}\times M_{kn}\to M_{mn}\) , wobei sich \(C=AB\) so berechnet, dass der Eintrag i,j in \(C\) das Standardskalarprodukt der i-ten Zeile von \(A\) mit der j-ten Spalte von \(B\) ist: \(c_{ij}=\sum_{k=1}^m a_{ik}b_{kj}\) .

Zum Beispiel \(c_{11}=a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31}\) .

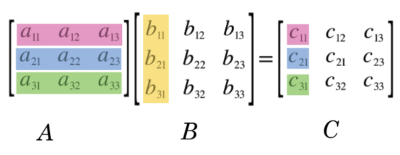
Anders ausgedrückt: Das Produkt einer Matrix mit einem Vektor ist die Linearkombination der Spaltenvekoren der Matrix mit den Vektoreinträgen als Koeffizienten. Zum Beispiel:

$$\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\ \begin{pmatrix}a\\ b\end{pmatrix} = a\cdot \begin{pmatrix}1\\ 3\end{pmatrix} + b \cdot \begin{pmatrix}2\\ 4\end{pmatrix}$$

Und übertragen auf Matrizenmultiplikation:

$$\begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}\ \begin{pmatrix}a & c\\ b & d\end{pmatrix} = ( a\cdot \begin{pmatrix}1\\ 3\end{pmatrix} + b \cdot \begin{pmatrix}2\\ 4\end{pmatrix} \quad c\cdot \begin{pmatrix}1\\ 3\end{pmatrix} + d \cdot \begin{pmatrix}2\\ 4\end{pmatrix} )$$

Die Matrizenmultiplikation ist assoziativ (d.h. \((AB)C = A(BC)\) ), aber nicht kommutativ (d.h. im Allgemeinen gilt nicht \(AB=BA\) ).

Eine Matrix \(A\) ist nilpotent, wenn es ein \(m\in\mathbb{N}\) gibt, so dass \(A^m = 0\) und \(A^{m-1}\neq 0\) . Für nilpotente Matrizen gilt:

• Das charakteristische Polynom ist von der Form \(x^n\) . Die einzige Nullstelle davon ist 0, also haben nilpotente Matrizen nur den Eigenwert 0.
• Da sie den Eigenwert 0 haben, ist ihr Kern nicht trivial und damit sind sie nicht invertierbar.
• Außerdem sind ihre Determinante und Spur jeweils 0.
• Sie sind entweder die Nullmatrix oder nicht diagonalisierbar.
• Sie haben keinen vollen Rang, d.h. ihre Spaltenvektoren sind linear abhängig.

Der Rang einer Matrix ist die Anzahl linear unabhängiger Spalten. Oder Zeilen, denn Spalten- und Zeilenrang sind immer gleich. (Die möglichen Ränge einer \(m\times n\) -Matrix sind also \(0\) bis \(\text{min}(m,n)\) .)

Die Spur einer Matrix ist die Summe der Diagonalelemente.

Der Kern einer Matrix \(A\) ist die Lösungsmenge von \(Av=0\) (d.h. alle Vektoren \(v\) , die diese Gleichung erfüllen).

Elementarmatrizen

Die Identitätsmatrix \(I_n\) ist die \(n\times n\) -Matrix, die in der Hauptdiagonale den Wert 1 hat und sonst 0. Zum Beispiel: $$I_1 = (1) \quad I_2 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix} \quad I_3 = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}$$

Elementarmatrizen unterscheiden sich von der Identitätsmatrix nur durch die Anwendung einer elementaren Zeilenumformung:

• \(P_{ij}\) Vertauschen der Zeilen \(i\) und \(j\)
• \(D_{i}(c)\) Multiplikation der Zeile \(i\) mit einem Skalar \(c\)
• \(T_{ij}(c)\) Addition des \(c\) -fachen der Zeile \(j\) zu einer anderen (nicht derselben!) Zeile \(i\)

Analog für Spalten. Diese Umformungen ändern den Rang einer Matrix nicht.

Transponierte, inverse und adjungierte Matrix

Die Transponierte \(A^T\) einer Matrix \(A\) ist diejenige Matrix, in der Zeilen und Spalten vertauscht sind (d.h. die 1. Zeile wird zur 1. Spalte usw.).

Die Inverse \(A^{-1}\) einer Matrix \(A\) ist diejenige Matrix, so dass \(A\cdot A^{-1} = A^{-1}\cdot A = I\) . Siehe Invertierbarkeit.

Die adjungierte Matrix einer komplexen Matrix \(A\) ist \(A^H=\overline{A}^T = \overline{A^T}\) .

Es gelten folgende Eigenschaften:

Transponierte	Adjungierte	Inverse
\((A+B)^T = A^T + B^T\)	\((A+B)^H = A^H + B^H\)
\((A\cdot B)^T = B^T \cdot A^T\)	\((A\cdot B)^H = B^H \cdot A^H\)	\((A\cdot B)^{-1} = B^{-1} \cdot A^{-1}\)
\((cA)^T = cA^T\)	\((cA)^H = \overline{c}A^H\)	\((cA)^{-1} = c^{-1}A^{-1}\)
\((A^T)^T = A\)	\((A^H)^H = A\)	\((A^{-1})^{-1} = A\)
\((A^{-1})^T = (A^T)^{-1}\)	\((A^{-1})^H = (A^H)^{-1}\)
\(\overline{A^T} = (\overline{A})^T\)		\(\overline{A^{-1}} = (\overline{A})^{-1}\)
\(\text{rang}({A^T}) = \text{rang}({A})\)	\(\text{rang}({A^H}) = \text{rang}({A})\)	\(\text{rang}({A^{-1}}) = \text{rang}({A})\)
\(\text{spur}({A^T}) = \text{spur}({A})\)	\(\text{spur}({A^H}) = \overline{\text{spur}({A})}\)
\(\text{det}({A^T}) = \text{det}({A})\)	\(\text{det}({A^H}) = \overline{\text{det}({A})}\)	\(\text{det}({A^{-1}}) = (\text{det}({A}))^{-1}\)

Eine reelle Matrix heißt

• symmetrisch, wenn \(A^T=A\) (bzw. wenn \(a_{ij}=a_{ji}\) für alle Einträge), und schiefsymmetrisch, wenn \(A^T=-A\)
• orthogonal, wenn \(A^T=A^{-1}\) (und damit \(A^T\cdot A = I\) ).

Eine komplexe Matrix heißt

• hermitesch, wenn \(A^T=\overline{A}\) (und damit \(A^H=A\) ), und schiefhermitesch, wenn \(A^T=-\overline{A}\)
• unitär, wenn \(A^H=A^{-1}\) (und damit \(A^H\cdot A = I\) ).

Reelle symmetrische Matrizen und komplexe hermitesche Matrizen haben viele Eigenschaften gemeinsam.

Determinante

Die Determinante ist eine eindeutige Abbildung \(M_{nn}(\mathbb{K})\to\mathbb{K}\) , die so definiert ist, dass sie genau dann 0 wird, wenn die Spalten der Matrix nicht linear unabhängig sind (die Matrix also nicht invertierbar ist): $$\text{det}(A) = \sum_{\sigma\in S_n}\text{sgn}(\sigma)a_{1\sigma(1)}\cdots a_{n\sigma(n)}$$

Wobei \(\sigma\in S_n\) eine Permutation der Indexmenge ist. Für die Berechnung der Determinante ist die sogenannte Leibniz-Formel aber nur bis \(n=2\) praktisch handhabbar.

Für \(n=1\) : trivial

$$\text{det}\begin{pmatrix} a \end{pmatrix} = a$$

Für \(n=2\) : einfach

$$\text{det}\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} = a_{11} a_{22} - a_{12} a_{21}$$ Das lässt sich gut nachvollziehen, denn wenn die Spaltenvektoren linear abhängig sind (und von 0 verschieden), heißt das es gibt ein \(c\in\mathbb{K}\) , so dass: $$\begin{pmatrix} a_{11} \\ a_{12} \end{pmatrix} = c\cdot \begin{pmatrix} a_{21} \\ a_{22} \end{pmatrix}$$ Also \(a_{11} = c\cdot a_{21}\) und \(a_{12} = c\cdot a_{22}\) , d.h. \(c=\dfrac{a_{11}}{a_{21}}\) und damit \(a_{12} = \dfrac{a_{11}}{a_{21}} a_{22}\) . Daraus ergibt sich \(a_{12} a_{21} = a_{11} a_{22}\) bzw. \(0 = a_{11} a_{22} - a_{12} a_{21}\) .

Für \(n=3\) : Sarrus-Regel

Man summiert:

• durchgezogene Linie: positives Produkt der Elemente
• gestrichelte Linie: negatives Produkt der Elemente

Funktioniert genauso, wenn man die ersten beiden Zeilen unter die Matriz schreibt.

Für \(n>3\) : Laplace-Entwicklung

Die Laplace-Entwicklung nach der i-ten Zeile ist die Summe aus folgendem Summanden für jedes Element \(a_{ij}\) : $$a_{ij}\cdot(-1)^{i+j}\cdot\text{det}(A_{ij})$$ Wobei \(A_{ij}\) die Matrix ist, die übrig bleibt, wenn man in \(A\) die i-te Zeile und j-te Spalte (also jeweils die Zeile und Spalte mit dem Eintrag \(a_{ij}\) ) entfernt.

Je mehr 0en in einer Zeile stehen, desto einfacher wird die Laplace-Entwicklung, deswegen macht es manchmal Sinn, erst elementare Zeilenumformungen auf die Matrix anzuwenden (wodurch sich die Determinante höchstens im Vorzeichen ändert, siehe Eigenschaften unten). Die Matrix wird also um \(n=1\) kleiner. Das wiederholt man so lange, bis \(n<3\) .

Analog funktioniert die Laplace-Entwicklung nach der j-ten Spalte.

Spezialfälle

• Wenn eine Zeile oder Spalte 0 ist, ist die Determinante 0.

• Wenn eine Zeile oder Spalte doppelt vorkommt, ist die Determinante 0.

• \(\text{det}(\text{normalform}(A))\) = Produkt der Diagonalelemente

  Die Determinante wird also genau dann 0, wenn das Produkt der Diagonalelemente der Normalform 0 ist, d.h. wenn mindestens eins der Diagonalelemente 0 ist. Die Determinanten erfasst damit, ob eine quadratische Matrix invertierbar (regulär) ist. Normalform bedeutet obere Dreiecksmatrix.

Eigenschaften

Die Determinante hat die folgenden Eigenschaften:

• \(\text{det}(I)=1\) (Identitätsmatrix)

• \(\text{det}(cA)=c^n\text{det}(A)\) (Skalarfaktor)

• \(\text{det}(AB)=\text{det}(A)\,\text{det}(B)\) für Matrizen über Integritätsbereichen

• \(\text{det}(A)=0\) genau dann, wenn \(\text{rang}(A) < n\)

  Ob \(\text{det}(A)=0\) oder nicht ändert sich also nicht durch Zeilenumformungen. Die Determinanten ist damit eine Invariante der Matrix.

  Für Elementarmatrizen gilt:

  • \(\text{det}(P_{ij}) = -1\) , also \(\text{det}(P_{ij}A)=-\text{det}(A)\)
  • \(\text{det}(D_{i}(c)) = c\) , also \(\text{det}(D_{i}(c)A)=c\cdot\text{det}(A)\)
  • \(\text{det}(T_{ij}(c)) = 1\) , also \(\text{det}(T_{ij}(c)A)=\text{det}(A)\)

Alternative Berechnungen

Aus den eben genannten Eigenschaften ergibt sich, dass man die Determinante einer Matrix \(A\) auch berechnen kann, indem man \(A\) in eine obere Dreiecksmatrix umformt. Die Determinante der oberen Dreiecksmatrix ist das Produkt ihrer Diagonalelemente und anhand dieser Determinante und den angewandten Elementarumformungen kann man die Determinante der ursprünglichen Matrix \(A\) berechnen.

Die Determinante ist außerdem das Produkt der Eigenwerte von \(A\) (in ihrer Vielfachheit).

Ist \(A\) symmetrisch, so gibt es eine zu \(A\) ähnliche Matrix \(B\) , deren Diagonalelemente genau die Eigenwerte von \(A\) sind. Denn die Eigenvektoren von \(A\) formen die Basis, unter der \(A\) eine Diagonalmatrix ist.

Invertierbarkeit

Eine \(n\times n\) -Matrix \(A\) ist genau dann invertierbar, wenn die Transformation, die sie darstellt, bijektiv ist.

Die folgenden Aussagen sind äquivalent:

• \(A\) ist invertierbar.
• \(\text{det}(A)\neq 0\) (d.h. wenn \(\text{det}(A)\) im Körper oder Ring, über dem die Matrix definiert ist, invertierbar ist)
• \(Ax=0\) hat nur die triviale Lösung \(x=0\) , d.h. \(\text{ker}(A)=\{0\}\) .
• 0 ist kein Eigenvektor von \(A\) .
• Die Spaltenvektoren von \(A\) sind linear unabhängig.
• \(A\) kann als endliches Produkt von Elementarmatrizen ausgedrückt werden.
• \(\text{rang}(A)=n\) , d.h. \(A\) hate vollen Rang.

Berechnung der Inversen

Für invertierbare \(2\times 2\) Matrizen \(\begin{pmatrix}a & b \\ c & d\end{pmatrix}\) gilt: \(\begin{pmatrix}a & b \\ c & d\end{pmatrix}^{-1} = \dfrac{1}{ad-bc}\begin{pmatrix}d & -b \\ -c & a\end{pmatrix}\)

Es gibt zwei Möglichkeiten, darauf zu kommen. In einfachen Fällen kann man \(A^{-1}A=I\) nutzen, um die Inverse zu berechnen.

Ist \(A\) zum Beispiel \(\begin{pmatrix}2 & 3 \\ 3 & 5\end{pmatrix}\) und man sucht \(A^{-1}=\begin{pmatrix}a & b \\ c & d\end{pmatrix}\) , dann gilt: $$\begin{pmatrix}a & b \\ c & d\end{pmatrix}\ \begin{pmatrix}2 & 3 \\ 3 & 5\end{pmatrix}=\begin{pmatrix}1 & 0 \\ 0 & 1\end{pmatrix}$$ Die Inverse findet man also durch Ausmultiplizieren und Lösen des Gleichungssystems.

Allgemeiner: Gilt \(AB=C\) und wendet man die gleichen Zeilenumformungen auf \(A\) und \(C\) an (mit dem Ergebnis \(A'\) und \(C'\) ), so ist \(A'B=C'\) . Da \(AA^{-1}=I\) , bedeutet das, dass man die Inverse einer Matrix bestimmen kann, indem man die gleichen Zeilenumformungen, die \(A\) in \(I\) überführen, ausführen kann, um \(I\) in \(A^{-1}\) zu überführen.

Praktisch heißt das, man bildet im obigen Beispiel die Matrix $$\begin{pmatrix} 2 & 3 & | & 1 & 0 \\ 3 & 5 & | & 0 & 1\end{pmatrix}$$ und formt sie durch elementare Umformungen um in $$\begin{pmatrix} 1 & 0 & | & 5 & -3 \\ 0 & 1 & | & -3 & 2\end{pmatrix}$$ woraus man die Inverse ablesen kann.

Matrizen als lineare Transformationen

Jede Matrix \(A\in M_{mn}(\mathbb{K})\) stellt eine lineare Abbildung \(f:\mathbb{K}^n\to\mathbb{K}^m\) zwischen endlichen Vektorräumen dar. Sie bildet die Vektoren \(x\in\mathbb{K}^n\) auf die Vektoren \(Ax\in\mathbb{K}^m\) ab, d.h. \(f(x)=Ax\) (die Multiplikation der Matrix \(A\) mit einem beliebigen Vektor \(x\) entspricht die Anwendung der Transformation auf diesen Vektor).

Linear ist die dargestellte Abbildung, weil die Matrizenmultiplikation sowohl Addition als auch Skalarmultiplikation respektiert:

• \(A(x+y) = Ax + Ay\)
• \(A(cx) = c(Ax)\)

Jeder Vektor \(x\) kann als Linearkombination \(c_1b_1+\cdots +c_nb_n\) von Basisvektoren \(b_1,\ldots,b_n\) dargestellt werden. Aufgrund der Linearität ergibt sich: $$Ax=A(c_1b_1+\cdots +c_nb_n)=c_1Ab_1+\cdots + c_nAb_n$$

Das bedeutet, dass eine lineare Abbildung vollständig dadurch bestimmt ist, worauf die Basisvektoren abgebildet werden. Die Darstellungsmatrix einer linearen Abbildung enthält als Spalten demnach genau die Vektoren \(f(b_1),\ldots,f(b_n)\) , auf die die Basisvektoren abgebildet werden. Was wiederum bedeutet, dass die Einträge der Darstellungsmatrix davon abhängen, welche Basis man betrachtet.

Zwei Matrizen stellen die gleiche lineare Abbildung dar, wenn sie ähnlich sind (bzw. kongruent im Fall von Bilinearformen).

Da endliche Vektorräume viel mehr sind als \(\mathbb{K}^n\) , z.B. wenn die Vektoren Funktionen sind, arbeitet man im allgemeinen nicht direkt mit den Vektoren, sondern mit ihren Koordinatenvektoren.

Aus der Interpretation von Matrizen als lineare Transformationen ergibt sich folgendes Bild:

• Die Elementarmatrizen entsprechen Basistransformationen (Rotation, Verschieben, Stauchen oder Strecken) und dass jede Matrix als Produkt von Elementarmatrizen darstellbar ist, bedeutet dass eine Transformation als Komposition von Basistransformationen beschrieben werden kann.

• In einem zweidimensionalen Raum kann man Linearität anschaulich so verstehen, dass die Transformation des Raumes seine Gridlinien parallel lässt und der Abstand zwischen ihnen überall gleich bleibt.

• Eine Diagonalmatrix stellt einer Transformation dar, die die Basisvektoren nur skaliert.

• Die Matrizenmultiplikation \(AB\) entspricht der Komposition der dargestellten Transformationen: \((f_A\circ f_B)(x) = f_A(f_B(x)) = A(Bx) = (AB)x\) . Das heißt das Produkt \(AB\) bedeutet, dass erst die Transformation \(B\) ausgeführt wird, dann \(A\) . Das macht auch intuitiv deutlich, warum \((AB)^{-1} = B^{-1}A^{-1}\) : $$\cdot \xrightarrow{B} \cdot \xrightarrow{A} \cdot \\ \xrightarrow[AB]{\qquad\ \quad} $$

• Die Inverse einer Matrix entspricht der inversen Transformation:

  • \(Ax=v\) bedeutet, dass die Tranformation \(A\) den Vektor \(x\) auf den Vektor \(v\) abbildet.
  • Daraus folgt \(x=A^{-1}v\) , d.h. man findet \(x\) , indem man die inverse Transformation \(A^{-1}\) auf \(v\) anwendet.

  Eine Matrix also genau dann invertierbar, wenn die dargestellte Transformation bijektiv ist.

• Der Rang einer Matrix entspricht der Anzahl der Dimensionen des Outputs der Transformation.

• Die Determinante einer Matrix ist der Faktor, um den ein Teil des Raumes durch die Transformation gestaucht oder gestreckt wird (z.B. der Inhalt einer Fläche im zweidimensionalen Raum oder das Volumen im dreidimensionalen Raum).

  • Ist die Determinante negativ, entspricht das einer Umkehrung der Orientierung des Raumes.
  • Ist die Determinante 0, heißt das, die Transformation bildet auf eine niedrigere Dimension ab. Man verliert also Informationen und kann die Transformation deswegen nicht rückgängig machen, d.h. die Matrix ist nicht invertierbar.
  • Die Darstellungsmatrizen einer Abbildung haben die gleiche Determinante. Die Determinante ist also unabhängig von der gewählten Basis und damit charakteristisch für die dargestellte Abbildung.

Basiswechsel

Eine Basiswechselmatrix \({}_BM_D\) ist diejenige Matrix bzw. Transformation, die einen Koordinatenvektor bezüglich \(B\) auf einen Koordinatenvektor bezüglich \(D\) abbildet: $${}_BM_D\cdot \text{Repr}_B(v) = \text{Repr}_D(v)$$ Ihre Spalten sind die Darstellungen \(\text{Repr}_D(b)\) der Basisvektoren \(b\in B\) bezüglich der Zielbasis \(D\) . Es gilt \({}_BM_D = ({}_DM_B)^{-1}\) und \({}_BM_D\cdot {}_DM_B = I\) . Und ist die Zielbasis die Einheitsbasis, ist es besonders einfach, denn es ist \(\text{Repr}_E(b)=b\) .

Um die Matrixdarstellung \(t\) einer gegebenen Transformation in ihre Matrixdarstellung \(t'\) bezüglich anderer Basen zu übersetzen, geht man in folgendem Diagramm den Weg von \(\mathbb{R}^n_{B'}\) zu \(\mathbb{R}^n_{D'}\) über \(t\) (hoch-rechts-runter).

$$\begin{matrix} & \mathbb{R}^n_B & \xrightarrow{t} & \mathbb{R}^n_D & \\ & & & & \\ {}_{B'}M_B & \big\uparrow & & \big\downarrow & {}_DM_{D'} \\ & & & & \\ & \mathbb{R}^n_{B'} & \xrightarrow[t']{} & \mathbb{R}^n_{D'} & \end{matrix}$$

Die Hintereinanderausführung dieser Schritte entspricht folgender Matrizenmultiplikation: $$t' = {}_DM_{D'}\cdot t\cdot {}_{B'}M_B$$ Wobei \({}_{B'}M_B = ({}_BM_{B'})^{-1}\) .

Das charakteristische Polynom einer Matrix

Für Matrizen \(A\in M_{nn}(\mathbb{K})\) berecht man das charakteristische Polynom wie folgt:

$$\chi_A=\text{det}(xI_n-A)$$

Die Nullstellen des charakteristischen Polynoms sind die Eigenwerte der Matrix.

Wenn \(A\) die Nullmatrix oder nilpotent ist, ist \(\chi_A=x^n\) (und umgekehrt).

Eigenwerte, Eigenvektoren, Eigenraum

Die Eigenvektoren \(v\) eines Endomorphismus \(f\) eines Vektorraums \(V\) bzw. seiner Matrixdarstellung \(A\) sind alle (vom Nullvektor verschiedene) Vektoren, die durch die Transformation nur gestaucht oder gestreckt werden, deren Richtung aber gleich bleibt. Der dazugehörige Eigenwert \(\lambda\) ist der Faktor der Stauchung oder Streckung. Formal: $$\quad f(v) = \lambda v \quad\text{bzw.}\quad Av = \lambda v$$

D.h. \(f(v)\) bzw. \(Av\) hat die gleiche Richtung wie \(v\) , nur um den Faktor \(\lambda\) gestaucht oder gestreckt.

• Eine Matrix muss keine Eigenvektoren besitzen - eine Rotation z.B. ändert die Richtung aller Vektoren im Raum.
• \(A\) und \(A^T\) haben möglicherweise unterschiedliche Eigenwerte.
• Sind die Eigenwerte verschieden, sind die dazugehörigen Eigenvektoren linear unabhängig.

Eigenwerte sind die Nullstellen des charakteristischen Polynoms. Eine Matrix \(A\in M_{nn}\) kann also höchstens \(n\) Eigenwerte haben. Wie oft eine Nullstelle vorkommt, nennt man die algebraische Vielfachheit des Eigenwerts.

Die Eigenvektoren zu einem Eigenwert spannen zusammen mit dem Nullvektor einen Unterraum auf, den Eigenraum: $$\begin{aligned}\text{Eigenraum}(f,\lambda) &= \{0\}\cup\{ v\in V \,|\, v\text{ ist ein Eigenvektor von }f \} \\ &= \{ v\in V \,|\, f(v) = \lambda v \}\\ &= \text{ker}(A-\lambda I_n) \end{aligned}$$ (Das heißt, der Eigenraum zum Eigenwert 0 ist \(\text{ker}(A)\) bzw. \(\text{ker}(f)\) .)

Die Dimension des Eigenraums ist die geometrische Vielfachheit des Eigenwerts.

Die Eigenwerte charakterisieren eine Matrix in ihren wesentlichen Eigenschaften.

Berechnung:

1. Um die Eigenwerte \(\lambda\) zu bestimmen, berechnet man die Nullstellen des charakteristischen Polynoms \(\text{det}(xI_n-A)\) .
2. Die Gleichung \(Av = \lambda v\) lässt sich äquivalent umformen zu: $$(A-\lambda I_n)v=0$$ Setzt man die Eigenwerte \(\lambda\) in diese Gleichung ein, erhält man ein Gleichungssystem, über das sich jeweils die zugehörigen Eigenvektoren \(v\) bestimmen lassen. Die müssen nicht eindeutig sein. (Bringt man $$A-\lambda I_n$$ in Treppennormalform und transponiert diese, dann sind die Spaltenvektoren die Basis des Eigenraums.)
3. Überprüfen kann man die gefundenen Eigenvektoren dann durch Einsetzen in \(Av = \lambda v\) .

Normalformen

Matrizen lassen sich nach Ähnlichkeit in Äquivalenzklassen einteilen, wobei eine Klasse alle Matrizen enthält, die den gleichen Endomorphismus darstellen. Technisch sind zwei Matrizen \(A,B\) ähnlich, wenn es eine invertierbare Matrix \(P\) gibt, so dass: $$A=P^{-1}BP$$ (Siehe Diagonalisierung.)

Matrizen lassen sich auch nach Kongruenz in Äquivalenzklassen (sogenannte Kongruenzklassen) einteilen: Zwei Matrizen \(A,B\) sind kongruent, wenn es eine invertierbare Matrix \(P\) gibt, so dass $$A=P^TBP$$

Da in der Regel \(P^T\neq P^{-1}\) , sind kongruente Matrizen in der Regel nicht ähnlich.

Ähnliche Matrizen haben:

• den gleichen Rang,
• die gleiche Determinante,
• das gleiche charakteristische Polynom und Minimalpolynom,
• die gleichen Eigenwerte,
• die gleiche Jordan-Normalform.

Diese Punkte sind alle notwendig, hinreichend ist aber nur der letzte. Das heißt:

• Wenn zwei Matrizen gleiche Ränge, Determinanten, charakteristische Polynome oder Eigenwerte haben, sind sie nicht zwangsläufig ähnlich. Aber wenn sie sich in diesen Eigenschaften unterscheiden, wissen wir, dass sie nicht ähnlich sind.
• Wenn zwei Matrizen die gleiche Jordan-Normalform haben, sind sie ähnlich.

Diagonalisierung

Zwei Matrizen \(A,B\) sind ähnlich, wenn es eine invertierbare Matrix \(P\) gibt, so dass: $$A=P^{-1}BP$$ Das bedeutet, dass \(A\) die gleiche Transformation wie \(B\) ausdrückt, nur in einer anderen Basis, wobei \(P\) die Basiswechselmatrix ist ( \(P\) ist nicht eindeutig, denn jedes Vielfache \(cP\) erfüllt die Gleichung auch). D.h. \(A\) und \(B\) stellen die gleiche Transformation dar, nur in unterschiedlichen Koordinatensystemen. Die Darstellungsmatrix eines Endomorphismus lässt sich also durch geschickte Wahl der Basis (und einen entsprechenden Basiswechsel) in eine Normalform bringen.

$$\begin{matrix} \text{Basis }1 & Px & \xrightarrow{A} & APx & \\ & & & & \\ & P\ \big\uparrow & & \big\downarrow\ P^{-1} & \\ & & & & \\ \text{Basis }2 & x & \xrightarrow[B]{} & P^{-1}APx & \end{matrix}$$

Berechnung: \(P\) kann man berechnen, indem man die Eigenwerte von \(A\) mit den dazugehörigen Eigenräumen findet und dann die Basisvektoren dieser Eigenräume als Spalten von \(P\) wählt:

• Eigenwerte von \(A\) bestimmen, d.h. die Nullstellen des charakteristischen Polynoms. Zerfällt das charakteristische Polynom nicht in Linearfaktoren, bzw. liegen nicht alle seine Nullstellen in \(\mathbb{K}\) , dann ist \(A\) nicht diagonalisierbar.
• Zu jedem Eigenwert \(\lambda\) den Eigenraum \(V_\lambda = \text{ker}(A-\lambda I)\) und eine Basis davon bestimmen. Ist \(\text{dim}(V_\lambda)\neq\text{Vielfachheit von }\lambda\) , dann ist \(A\) nicht diagonalisierbar.
• Die Basisvektoren der Eigenräume sind die Spalten von \(P\) . Wenn \(P\) orthogonal sein soll, muss man entsprechend die Orthonormalbasis der Eigenräume bilden, siehe Gram-Schmidt-Verfahren zur Orthogonalisierung.
• Die Diagonalmatrix ist dann \(P^{-1}AP\) .

Im Prinzip ist es ein Basiswechsel, bei dem man weder die Zielbasis noch die Zielmatrix kennt. Man weiß aber, dass ähnliche Matrizen (unter Berücksichtigung des Basiswechsels) die gleichen Eigenvektoren haben: Ist \(x\) ein Eigenvektor von \(A\) , d.h. \(Ax=\lambda x\) , dann ist \(P^{-1}x\) ein Eigenvektor von \(B\) , denn: $$B(P^{-1}x) = (P^{-1}AP)(P^{-1}x) = P^{-1}A(PP^{-1})x = P^{-1}Ax = P^{-1}\lambda x$$

Eine Diagonalmatrix stellt daher eine Transformation dar, die Vektoren nur skaliert.

Eine Matrix auf jeden Fall diagonalisierbar, wenn

• sie symmetrisch ist (d.h. \(A^T=A\) ) - die Diagonalelemente sind dann genau die Eigenwerte der Matrix;
• sie die maximale Anzahl Eigenwerte hat (= Anzahl der Dimensionen des Vektorraums), denn dann sind die zugehörigen Eigenvektoren linear unabhängig und es gibt eine Basis aus Eigenvektoren, d.h. der Vektorraum ist die Summe der Eigenräume;
• das charakteristische Polynom in Linearfaktoren zerfällt und die algebraische und geometrische Vielfachheit der Eigenwerte übereinstimmen.

Treppennormalform

• Alle Nullreihen stehen ganz unten.
• In jeder Zeile ist der von links erste Eintrag ungleich 0 eine 1. Das sind die Pivot-Positionen.
• Stufung: Jede Pivot-Position ist rechts von der Pivot-Position der Zeile darüber.
• Daraus folgt, dass alle Einträge unter den Pivot-Positionen 0 sind. In der reduzierten Treppennormalform sind auch alle Einträge über den Pivot-Positionen 0.

Die Treppennormalform erleichtert das Lösen eines linearen Gleichungssystems.

Beispiele: $$\left(\begin{matrix} 1 & \ast & \ast & \ast \\ 0 & 0 & 1 & \ast \\ 0 & 0 & 0 & 1 \end{matrix}\right) \qquad \left(\begin{matrix} 1 & \ast & \ast \\ 0 & 1 & \ast \\ 0 & 0 & 0 \end{matrix}\right) \qquad \left(\begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}\right)$$

Berechnung: Gaußsches Eliminationsverfahren

Jordan-Normalform

Ist eine Matrix nicht diagonalisierbar, will man einer Diagonalform möglichst nahe kommen. Das kann man mit der Jordan-Normalform.

Eine Jordan-Matrix enthälten auf der Diagonalen Jordan-Blöcke und sonst 0. Ein Jordan-Block ist eine quadratische Matrix mit einem Eigenwert auf der Diagonalen, 1 auf einer der Nebendiagonalen und sonst 0. Zum Beispiel:

• \(\,\,(\lambda_1)\)
• \(\,\begin{pmatrix} \lambda_2 & 1 \\ 0 & \lambda_2 \end{pmatrix}\text{ oder }\begin{pmatrix} \lambda_2 & 0 \\ 1 & \lambda_2 \end{pmatrix}\)
• \(\begin{pmatrix} \lambda_3 & 1 & 0 \\ 0 & \lambda_3 & 1 \\ 0 & 0 & \lambda_3 \end{pmatrix}\text{ oder }\begin{pmatrix} \lambda_3 & 0 & 0 \\ 1 & \lambda_3 & 0 \\ 0 & 1 & \lambda_3 \end{pmatrix}\)

Die Reihenfolge der Blöcke in einer Jordan-Matrix ist egal.

Berechnung: Für eine Matrix \(A\in M_{nn}(\mathbb{K})\) .

1. Eigenwerte der Matrix berechnen, d.h. die Nullstellen des charakteristischen Polynoms \(\chi_A=\text{det}(xI_n-A)\) bestimmen, zusammen mit ihrer algebraischen Vielfachheit. (Wenn \(\chi_A\) nicht in Linearfaktoren über \(\mathbb{K}\) zerfällt, also z.B. das Produkt von Polynomen ist, von denen mindestens eins keine Nullstellen in \(\mathbb{K}\) hat, dann hat die Matrix keine Jordan-Normalform in \(\mathbb{K}\) .)
2. Für jeden Eigenwert \(\lambda\) :
   • Wenn die algebraische Vielfachheit 1 ist, dann gibt es einen Jordan-Block der Größe 1, also \((\lambda)\) .
   • Ansonsten berechne die Haupträume \(H_k = \text{ker}((A-\lambda I_n)^k)\) zu \(\lambda\) , wobei $$\{0\} \subset H_1 \subset H_2 \subset \ldots$$ bis \(\text{dim}(H_k)\) die algebraische Vielfachheit von \(\lambda\) ist. Dann wissen wir: Es gibt \(\text{dim}(H_1)\) viele Jordan-Blöcke für \((\lambda)\) und davon sind \(\text{dim}(H_{i+1}) - \text{dim}(H_i)\) viele Jordan-Blöcke von mindestens der Größe \(i\) .
3. Aus diesen Informationen können wir die Jordan-Normalform bauen.

Matrizen als Gleichungssysteme

Wenn wir ein System von \(m\) linearen Gleichungen mit \(n\) Unbekannten \(x_1,\ldots,x_n\) haben: $$\begin{aligned}a_{11}x_1+\cdots +a_{1n}x_n & = b_1\\ & \ \vdots \\ a_{m1}x_1+\cdots +a_{mn}x_n & = b_m\end{aligned}$$ Dann kann das dargestellt werden als Matrizengleichung \(Ax=b\) mit folgender Matrix \(A\) und Vektoren \(b\) und \(x\) : $$A = \begin{pmatrix} a_{11} & \ldots & a_{1n} \\ \vdots & \cdots & \vdots \\ a_{m1} & \ldots & a_{mn} \end{pmatrix},\quad b = \begin{pmatrix} b_1 \\ \vdots \\ b_m \end{pmatrix},\quad x = \begin{pmatrix} x_1 \\ \vdots \\ x_n \end{pmatrix}$$

Ist \(m>n\) , also wenn es mehr Gleichungen als Unbekannte gibt, gibt es oft keine Lösung.

Ist \(m<n\) , also wenn es mehr Unbekannte als Gleichungen gibt, gibt es oft mehrere (ggf. unendlich viele) Lösungen.

Im Fall \(m=n\) ist \(A\) eine quadratische \(n\times n\) -Matrix. Wenn \(A\) invertierbar ist, dann ist die Lösung des Gleichungssystems \(x=A^{-1}b\) (denn \(Ax=A(A^{-1}b)=Ib=b\) ). Die Lösung des Gleichungssystems zu finden, hängt also eng mit der Frage zusammen, ob \(A\) invertierbar ist.