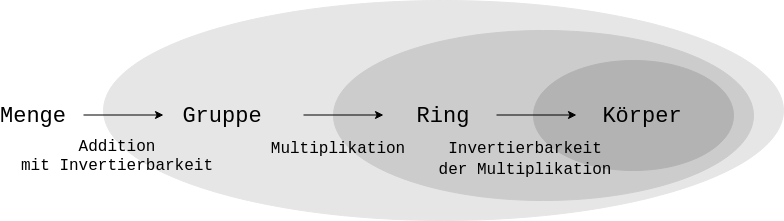
Algebraische Strukturen

Gruppen, Ringe, Körper, Vektorräume und strukturerhaltende Abbildungen.

Algebraische Strukturen sind Mengen von mathematischen Objekten zusammen mit Verknüpfungen, unter denen die Menge abgeschlossen ist und die bestimmte Bedingungen erfüllen.

Gruppen

Eine Gruppe $(M,\ast)$ ist eine Menge $M$ mit einer Verknüpfung $\ast$ , so dass:

$\ast$ assoziativ ist, d.h. $a\ast(b\ast c) = (a\ast b)\ast c$
es ein neutrales Element $e$ bezüglich $\ast$ gibt, d.h. $a\ast e=a=e\ast a$
jedes $a\in M$ ein inverses Element $a'$ besitzt, d.h. $a\ast a' = a'\ast a = e$

Notation: $-a$ für additive Verknüpfungen und $a^{-1}$ für multiplikative Verknüpfungen.

Neutrales Element und inverse Elemente sind eindeutig.

In einer abelsche Gruppe ist die Verknüpfung außerfdem kommutativ, d.h. $a\ast b = b\ast a$ . Die Verknüpfung wird oft additiv interpretiert für kommutitative Gruppen und multiplikativ für andere.

Beispiele:

$(\mathbb{Z},+)$ und $n\mathbb{Z} = \{\ldots,-2n,-n,0,n,2n,\ldots\}$ als Untergruppe
$(\{1,-1\},\cdot)$
$(\mathbb{Q},+)$
$(\mathbb{R},+)$
$(\mathbb{Q}\backslash\{0\},\cdot)$
$(\mathbb{R}\backslash\{0\},\cdot)$
Abbildungen mit Komposition, z.B. $(\mathbb{R}\times\mathbb{R}\to\mathbb{R},\circ)$

Keine Gruppe:

$(\mathbb{N},+)$ (kein neutrales Element, wenn $0\notin\mathbb{N}$ , und keine inversen Elemente)
$(\mathbb{N},\cdot)$ (keine inversen Elemente, außer für 1 und -1)
$(\mathbb{Z},\cdot)$
$(\mathbb{Q},\cdot)$
$(\mathbb{R},\cdot)$

Symmetrische Gruppen

Ein wichtiges Beispiel für nicht-kommutative Gruppen sind die symmetrischen Gruppen $(S_n, \circ)$ : die Gruppe aller Permutationen von $n$ Objekten. Wobei $S_n$ die Menge der bijektiven Abbildungen auf $\{1,\ldots,n\}$ ist und die Verknüpfung $\circ$ die Hintereinanderausführung zweier solcher Abbildungen. Das neutrale Element ist die Abbildung $\text{id}:x\mapsto x$ .

$S_n$ ist für $n > 2$ nicht abelsch, d.h. $\circ$ ist in dem Fall nicht für alle Abbildungen kommutativ.

Transpositionen sind Permutationen, die genau zwei Elemente vertauschen. Jede Permutation kann als Komposition von Transpositionen dargestellt werden.

Ringe

Ein Ring $(M,+,\cdot)$ ist eine abelsche Gruppe $(M,+)$ mit einer weiteren Verknüpfung $\cdot$ , die

assoziativ ist, d.h. $a\cdot(b\cdot c) = (a\cdot b)\cdot c$
distributiv ist über $+$ , d.h. $a\cdot(b+c) = (a\cdot b)+(a\cdot c)$ , also dass beide Verknüpfungen miteinander verträglich sind
aber nicht kommutativ sein muss, nicht zwangsläufig ein neutrales Element bezüglich $\cdot$ (d.h. ein Einselement) haben muss und bezüglich der Elemente deswegen nicht unbedingt invertierbar sind.

Die Einheitengruppe $R^\times$ eines Rings $R$ mit Einselement ist die Menge aller Elemente, die bezüglich $\cdot$ invertierbar sind, also $\{a\in R\,|\, \text{es existiert ein } b\in R \text{ mit } ab = ba = 1\}$ . (Zusammen mit $\cdot$ bildet diese Menge eine Gruppe.)

Beispiele:

$(\mathbb{Z},+,\cdot)$ , es ist $\mathbb{Z}^\times = \{1,-1\}$
Die Menge $M_{nn}(\mathbb{K})$ der $n\times n$ -Matrizen über $\mathbb{K}$ mit Matrizenaddition und Matrizenmultiplikation (nicht kommutativ). Es ist $M_{nn}(\mathbb{K})^\times = \{A\,|\,\text{det}(A)\neq 0\}$ .
Eine Menge von Abbildungen mit punktweiser Definition von Addition und Multiplikation (siehe z.B. Polynomringe).

In einem Ring kann es sein, dass es Nullteiler gibt, also von 0 verschiedene Elemente $a,b\in M$ mit $ab=0$ (z.B. im Ring $M_{nn}(\mathbb{K})$ ). Ein kommutativer Ring mit Einselement, aber ohne Nullteiler, heißt Integritätsbereich oder Integritätsring. Beispiele sind alle Körper, denn in Körpern gibt es außer der 0 keine Nullteiler.

Restklassenringe

Der Restklassenring $(\mathbb{Z}/n\mathbb{Z},+,\cdot)$ ist die Menge der Reste bei Division durch $n$ , also $\{0,1,\ldots,n-1\}$ , wobei die Elemente $k$ nicht die natürlichen Zahlen sind, sondern Stellvertreter für die jeweilige Restklasse $k+n\mathbb{Z}$ (z.B. steht $1$ stellvertretend für alle Zahlen, die bei Division durch $n$ den Rest 1 lassen). Addition und Multiplikation liefern immer ein Element der Menge, z.B. ist $3 + 1 = 0$ in $\mathbb{Z}/4\mathbb{Z}$ .

Ein Element $a$ ist invertierbar genau dann, wenn $\text{ggT}(a,n)=1$ .

Für jede natürliche Zahl $n$ ist $(\mathbb{Z}/n\mathbb{Z},+,\cdot)$ ein kommutativer Ring mit Einselement.

Das Nullelement ist $0=n\mathbb{Z}$ .
Das Einselement ist $1=1+n\mathbb{Z}$ .

Ist $n$ eine Primzahl, ist der Restklassenring ein endlicher Körper. Ist $n$ keine Primzahl, ist er kein Körper (denn er hat von Null verschiedene Nullteiler, z.B. 2 in $(\mathbb{Z}/4\mathbb{Z},+,\cdot)$ , denn $2\cdot 2 = 0$ ).

Polynomringe

Ein Polynomring $(R[x],+,\cdot)$ ist eine Menge von Polynomfunktionen $x\mapsto\sum_{k=0}^n a_kx^k$ über $R$ zusammen mit Polynom-Addition und -Multiplikation:

$(p+q)(x):=p(x)+q(x)$
$(p\cdot q)(x):=p(x)\cdot q(x)$

Das Einselement ist $x\mapsto x^0 = 1$ .

Ist $(R,+,\cdot)$ ein Integritätsring, so ist auch $(R[x],+,\cdot)$ einer, mit der Einheitengruppe $R[x]^\times = \{ x\mapsto a \,|\, a\in R^\times \}$ .

Körper

Ein Körper $(\mathbb{K},+,\cdot)$ (field) ist eine Menge $\mathbb{K}$ mit zwei Verknüpfungen $+$ und $\cdot$ , und zwei verschiedenen Elementen 0 und 1, so dass:

$+$ assoziativ und kommutativ ist
0 das neutrale Element bezüglich $+$ ist und jedes Element von $\mathbb{K}$ invertierbar ist, d.h. $a+(-a)=0$
$\cdot$ assoziativ und kommutativ ist
1 das neutrale Element bezüglich $\cdot$ ist und jedes Element von $\mathbb{K}$ invertierbar ist, d.h. $a\cdot a^{-1}=1$
$\cdot$ distributiv ist über $+$ , d.h. $a\cdot (b+c)=a\cdot b + a\cdot c$

Das heißt: $(\mathbb{K},+)$ und $(\mathbb{K}\backslash\{0\},\cdot)$ sind abelsche Gruppen.

Beispiele:

$\mathbb{F}_p = (\mathbb{Z}/p\mathbb{Z},+,\cdot)$ (sogenannte Galoiskörper, wobei $p$ eine Primzahl ist)
$(\mathbb{Q},+,\cdot)$
$(\mathbb{R},+,\cdot)$
$(\mathbb{\mathbb{R}^2},+,\cdot)$ mit
- $(a,b)+(c,d) = (a+c,b+d)$
- $(a,b)\cdot(c,d) = (ac-bd,ad+bc)$
- $i = (0,1)$
- $1 = (1,0)$

(Siehe Konstruktion der komplexen Zahlen.)

Keine Körper:

$(\mathbb{N},+,\cdot)$ (nicht alle Elemente sind invertierbar)
$(\mathbb{Z},+,\cdot)$ (nicht alle Elemente sind bezüglich der Multiplikation invertierbar)

Vektorräume

Ein Vektorraum $(V,+,\cdot)$ (vector space oder linear space) über dem Körper $\mathbb{K}$ ist eine Menge $V$ von Vektoren zusammen mit zwei Operationen: Addition ( $V\times V\to V$ ) und Skalarmultiplikation ( $\mathbb{K}\times V\to V$ ), die die folgenden Axiome erfüllen.

Addition ist kommutativ und assoziativ, hat ein neutrales Element (den Nullvektor 0) und jeder Vektor ist bezüglich Addition invertierbar.
Skalarmultiplikation ist assoziativ und hat ein neutrales Element (den Skalar 1).
Skalarmultiplikation distribuiert über Addition.

Wir verbinden also eine abelsche Gruppe $(V,+)$ mit einem Körper $\mathbb{K}$ , dessen Multiplikation kompatibel mit der Addition in $V$ ist.

Vektoren sind die Elemente eines Vektorraums; sie können so ziemlich alles sein, solange Addition und Skalarmultiplikation so definiert sind, dass sie die obigen Axiome erfüllen: Matrizen, Funktionen, Koordinaten im n-dimensionalen Raum ( $\mathbb{R}^n$ oder $\mathbb{C}^n$ ; hier ist der Vektorraum im Prinzip ein n-dimensionaler Körper, wobei die Multiplikation keine Verknüpfung von Körperelementen ist, sondern deren Stauchung oder Streckung durch einen Skalar). Entscheidend ist nicht so sehr die Form von Vektoren, sondern ihre Eigenschaften. Der Gedanke hinter dem Begriff des linearen Raums ist, dass Vektoren all das sind, wovon man Linearkombinationen bilden kann.

Eine Menge von Vektoren ist linear unabhängig, wenn keiner der Vektoren eine Linearkombination der anderen ist. Das ist äquivalent zu der Bedingung, dass sie sich zum Nullvektor nur mittels Koeffizienten $a_i=0$ linearkombinieren lassen. Oder technisch:

Ein endliches System von Vektoren $(v_1,\ldots,v_n)$ ist linear unabhängig, wenn aus $\sum_{i=1}^n a_i v_i = 0$ folgt, dass $a_1=\ldots=a_n=0$ .
Ein unendliches System von Vektoren $(v_i)_{i\in I}$ ist linear unabhängig, wenn für jede endliche Teilmenge $J$ von $I$ aus $\sum_{j\in J} a_j v_j=0$ folgt, dass $a_j=0$ für alle $j\in J$ .

Eine Basis eines Vektorraums ist eine Menge linear unabhängiger Vektoren, mit deren Hilfe sich jeder Vektor eindeutig as Linearkombination darstellen lässt. Alle Basen eines Vektorraums haben die gleiche Anzahl Basisvektoren; das ist die Dimension des Vektorraums.

Koordinatenvektoren

Jeder Vektor $v$ eines n-dimensionalen Vektorraums ist eine Linearkombination der Basisvektoren. Der Koordinatenvektor, der $v$ bezüglich einer Basis $B$ repräsentiert, ist derjenige Vektor $\text{Repr}_B(v)$ in $\mathbb{R}^n$ , dessen Elemente die Koeffizienten der Linearkombination bezüglich der Basis $B$ sind.

Beispiele:

Ist $v=(x^2-x)\in \mathbb{R}[x]$ , dann ist sein Koordinatenvektor $\text{Repr}_E(v) = \begin{pmatrix}1\\1\\0\end{pmatrix}$ bezüglich der Standardbasis $\langle x^2,x^1,x^0\rangle$ , weil $v=x^2-x= 1\cdot x^2 - 1\cdot x^1 + 0\cdot x^0$ .
Ist $v=\begin{pmatrix}2 \\-1 \end{pmatrix}\in\mathbb{R}^2$ , dann ist der Koordinatenvektor $\text{Repr}_E(v)$ bezüglich der Standardbasis $E$ trivialerweise gleich $v$ , weil $\begin{pmatrix}2 \\-1 \end{pmatrix} = 2\begin{pmatrix}1 \\0 \end{pmatrix} -1 \begin{pmatrix}0 \\1 \end{pmatrix}$ . Der Koordinatenvektor von $v$ bezüglich einer anderen Basis, zum Beispiel $B=\langle\begin{pmatrix}2 \\1 \end{pmatrix}, \begin{pmatrix}-2 \\4 \end{pmatrix}\rangle$ ist dann $\text{Repr}_B(v)=\begin{pmatrix}a \\b \end{pmatrix}$ , wobei $a,b$ die Koeffizienten der Linearkombination der Basisvektoren $B$ ist, die $v$ ergibt, d.h. die Lösung von $\begin{pmatrix}2 \\-1 \end{pmatrix} = a\begin{pmatrix}2 \\1 \end{pmatrix} + b \begin{pmatrix}-2 \\4 \end{pmatrix}$ .

Untervektorräume

Untervektorräume sind Teilmengen von Vektorräumen, die selber wieder eine Vektorraum sind. D.h. zu einem Vektorraum $(V,+,\cdot)$ über einem Körper $\mathbb{K}$ ist $(U,+,\cdot)$ mit $U\subseteq V$ ein Untervektorraum, wenn:

$0_V\in U$
$cv \in U$ für alle $v \in U, c\in\mathbb{K}$
$v+w \in U$ für alle $v,w \in U$

Jeder Vektorraum $V$ hat die trivialen Unterräume $\{0\}$ und $V$ .

Ein Untervektorraum $U$ heißt $f$ -invariant, wenn für alle $u\in U$ gilt, dass $f(u)\in U$ (d.h. $f$ führt nicht aus $U$ heraus).

Außerdem gilt:

Der Kern einer linearen Abbildung $V\to W$ ist ein Unterraum von $V$ .
Das Bild einer linearen Abbildung $V\to W$ ist ein Unterraum von $W$ .
Wenn $U_1$ und $U_2$ Unterräume von $V$ sind, so ist auch $U_1\cap U_2$ ein Unterraum von $V$ .
Wenn $U$ ein Unterraum von $V$ ist, kann $V\backslash U$ nicht auch Unterraum sein (weil $0\in U$ , also $0\notin V\backslash U$ ). Es gibt aber einen zu $U$ komplementären Unterraum $U'$ , so dass $U\cap U'=\{0\}$ und $V=U+U'=\{u+u'\,|\,u\in U,u'\in U'\}$ . ( $U+U'$ entspricht dem Schnitt aller Unterräume, in denen $U$ und $U'$ enthalten sind.)
Die Linearkombinationen von Vektoren $v_1,\ldots,v_n\in V$ bilden einen Unterraum von $V$ .

Beispiele:

$\mathbb{R}$ hat nur die trivialen Unterräume.
$\mathbb{R}^2$ hat zusätzlich alle Geraden durch den Nullpunkt als Unterräume, d.h. alle $U=\{(x,y)\,|\,y = ax, \text{ wobei } a\in\mathbb{R}\}$ .
$\mathbb{R}^3$ hat zusätzlich alle Geraden und Ebenen durch den Nullpunkt als Unterräume. (Die Ebenen sind alle $U=\{(x,y,z)\,|\, ax+by+cz=0, \text{ wobei } a,b,c\in\mathbb{R}\}$ .)
Nicht-triviale Untervektorräume von $\mathbb{C}$ sind $\mathbb{R}$ und die imaginären Zahlen $i\mathbb{R}=\{ix\,|\,x\in\mathbb{R}\}$ .
Der Vektorraum der Polynome vom Grad $\leq n$ hat als Unterräume die Vektorräume der Polynomen vom Grad $\leq k$ mit $k\leq n$ . (Die Polynome vom Grad $n$ sind kein Vektorraum, weil sie nicht unter Addition abgeschlossen sind, z.B. ist die Summe von $x^2 + x$ und $-x^2$ das Polynom $x$ von einem anderen Grad.)
Der Vektorraum der reellen Funktionen hat als Unterräume den Vektorraum der linearen Funktionen, den der stetigen Funktionen, sowie den der differenzierbaren und den der integrierbaren Funktionen.
Der Vektorraum quadratischer Matrizen hat als Unterräume den der symmetrischen und den der schiefsymmetrischen Matrizen.

Quotientenvektorraum

Wenn $V,U$ Vektorräume sind mit $U\subseteq V$ , ist der Quotientenvektorraum $(V/U,+,\cdot)$

die Menge $V/U = \{ v + U\,|\, v\in V \}$ , d.h. die Menge aller um den Vektor $v$ verschobenen Unterräume $v+U=\{v+u\,|\,u\in U\}$ , zusammen mit
der Addition $(v+U)+(w+U)=(v+w)+U$ und
der Skalarmultiplikation $c(v+U)=cv+U$ .

Beispiel: Für eine Gerade $U$ im $\mathbb{R}^2$ besteht $\mathbb{R}^2/U$ aus allen zu $U$ parallelen Geraden (und analog für Ebenen im $\mathbb{R}^3$ ).

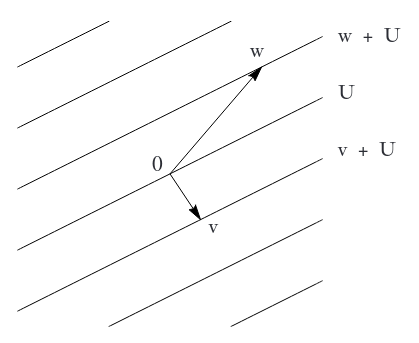
Beispiel Quotientenvektorraum

(Quelle: Erste Hilfe Lineare Algebra)

Anders betrachtet ist $v+U$ die Äquivalenzklasse aller Vektoren $w_1,w_2$ , die sich nur durch einen Vektor aus $U$ unterscheiden (d.h. $w_1-w_2\in U$ ).

Das Nullelement ist $0+U$ und es gilt $\text{dim}(V/U) = \text{dim}(V) - \text{dim}(U)$ .

TODO:

Der Quotientenvektorraum ist der Lebensraum der Homomorphismen auf $V$ , die auf $U$ verschwinden.
$(V/U,+)$ ist die Faktorgruppe der Gruppe $(V,+)$ .

Skalarprodukt

Das Skalarprodukt (dot product oder inner product) bildet zwei Vektoren auf ein Skalar ab und liefert damit eine zusätzliche Struktur, die es erlaubt geometrische Maße wie Längen und Winkel zu definieren, indem es eine Norm induziert.

Technisch ist das Skalarprodukt eines Vektorraums $(V,+,\cdot)$ über dem Körper $\mathbb{K}$ eine Abbildung $\langle\cdot,\cdot\rangle:V\times V\to \mathbb{K}$ , die für alle für $v,w\in V$ folgende Eigenschaften erfüllt:

Positive Definitheit: $\langle v,v\rangle > 0$ (bzw. $\langle v,v\rangle \geq 0$ , aber $\langle v,v\rangle = 0$ nur für $v = 0$ )
Symmetrie: $\langle v,w\rangle = \langle w,v\rangle$
Bilinearität: $\langle v,\cdot\rangle$ und $\langle \cdot, v\rangle$ sind linear (d.h. das Skalarprodukt ist eine Bilinearform)

Beispiele kanonischer Skalarprodukte:

$\mathbb{R}^n$ : $\langle x,y\rangle := \sum_{i=1}^n x_i y_i = x^Ty$
$\mathbb{C}^n$ : $\langle x,y\rangle := \sum_{i=1}^n x_i \overline{y_i}$
Reellwertige Funktionen $C[a,b]$ : $\langle f,g\rangle := \int_a^b f(x)g(x) dx$ (stetig und damit auch integrierbar, umfasst auch die Polynome über $\mathbb{R}$ )
Komplexwertige Funktionen $C[a,b]$ : $\langle f,g\rangle := \int_a^b f(x)\overline{g(x)} dx$

Euklidische Vektorräume

Ein Euklidischer Vektorraum ist ein reeller Vektorraum mit einem Skalarprodukt.

Die Norm (d.h. die Länge eines Vektors), die von einem Skalarprodukt über $\mathbb{K}=\mathbb{R}$ oder $\mathbb{K}=\mathbb{C}$ induziert wird, ist folgende: $$\|v\|=\sqrt{\langle v,v\rangle}$$

Ein Vektor ist normalisiert, wenn er Länge 1 hat. Jeder Vektor $v$ lässt sich normalisieren zu $\dfrac{v}{\|v\|}$ . (Das funktioniert mit dem Skalarprodukt, ist aber allgemein mit Bilinearformen nicht immer möglich.)

Zwei Vektoren $v,w$ sind orthogonal, wenn $\langle v,w\rangle = 0$ .

Orthonormalbasen (Gram-Schmidt-Verfahren)

Zu einer beliebigen Basis $\{v_1,v_2,v_3,\ldots,v_n\}$ lässt sich eine orthonormale Basis $\{w_1,w_2,w_3,\ldots,w_n\}$ konstruieren, indem man jeden Vektor zu den vorherigen orthogonalisiert und dann normalisiert:

$w_1=\dfrac{v_1}{\|v_1\|}$
$w_2'=v_2 - \langle w_1,v_2\rangle w_1$
$w_2=\dfrac{w_2'}{\|w_2'\|}$
$w_3'=v_3 - \langle w_1,v_3\rangle w_1 - \langle w_2,v_3\rangle w_2$
$w_3=\dfrac{w_3'}{\|w_3'\|}$
…
$w_n'=v_n - \sum_{i=1}^{n-1}\langle w_i,v_n\rangle w_i$
$w_n=\dfrac{w_n'}{\|w_n'\|}$

Strukturerhaltende Abbildungen

Lineare Abbildungen

Ein Homomorphismus zwischen zwei algebraischen Strukturen $\mathbf{A}=(A,(\circ_\mathbf{A})_i)$ und $\mathbf{B}=(B,(\circ_\mathbf{B})_i)$ ist eine Abbildung $f:A\to B$ , die die neutralen Elemente von $\mathbf{A}$ auf die neutralen Elemente von $\mathbf{B}$ abbildet und die die algebraische Struktur erhält, also so dass für alle Operationen $\circ_\mathbf{A}$ und $\circ_\mathbf{B}$ gilt: $$f(x\circ_\mathbf{A} y)=f(x)\circ_\mathbf{B} f(y)$$

Ein bijektiver Homomorphismus heißt Isomorphismus.

Ein Homomorphismus $f:A\to A$ , der eine algebraische Struktur auf sich selbst abbildet, heißt Endomorphismus (oder Automorphismus, wenn er bijektiv ist).

Eine Abbildung $f$ lässt sich als Matrix $A$ darstellen, so dass $f(x)=Ax$ (siehe Matrizen als lineare Transformationen).

Die Matrixdarstellung einer injektiven Abbildung hat linear unabhängige Spalten.
Die Matrixdarstellung einer surjektiven Abbildung hat linear unabhängige Zeilen.

Das Lösen eines linearen Gleichungssystems $Ax=b$ entspricht also dem Finden des Urbilds von $b$ .

Wie viele Informationen bei einer Abbildung $f:A\to B$ verloren gehen, kann am Kern der Abbildung abgelesen werden. Der Kern sind all die Elemente aus $A$ , die auf Null abgebildet werden, also $\text{ker}(f)=\{x\in A\,|\,f(x)=0_\mathbf{B}\}$ . Der Kern enthält immer wenigstens $0_\mathbf{A}$ . Wenn er keine weiteren Elemente enthält, ist die Abbildung injektiv, d.h. es gehen keine Informationen verloren.

Zum Beispiel ist eine Abbildung nicht injektiv, wenn es unterschiedliche Elemente $x,x'\in A$ gibt, so dass $f(x)=f(x')$ , also $f(x)-f(x')=0$ . Bei einer linearen Abbildung heißt das $f(x-x')=0$ , d.h. $x-x'$ liegt im Kern; der Unterschied zwischen $x$ und $x'$ geht also bei der Abbildung verloren.

Das erklärt auch intuitiv, warum für eine lineare Abbildung $f:A\to B$ gilt: $$\text{dim}(\text{ker}(f)) + \text{dim}(\text{im}(f)) = \text{dim}(A)$$ Die Dimension von $B$ (dem Bild von $f$ , also $\text{dim}(\text{im}(f))$ ) ist die Dimension von $A$ minus die Dimensionen, die durch die Abbildung verloren gehen. Obwohl $\text{dim}(B)$ größer sein kann als $\text{dim}(A)$ , kann $f$ also nur in einen höchstens $\text{dim}(A)$ -dimensionalen Unterraum von $B$ abbilden.

Ist $\mathbf{A}$ ein Vektorraum, dann bilden der Kern und das Bild einer Abbildung zusammen mit den Operationen in $\mathbf{A}$ einen Untervektorraum von $\mathbf{A}$ .

Bilinearformen

Eine Bilinearform verallgemeinert die Eigenschaften eines Vektorraumhomomorphismus auf zweistellige Abbildungen und bedeutet dann Linearität in beiden Komponenten:

Seien $V,W$ Vektorräume über einem Körper $\mathbb{K}$ . Dann ist eine Abbildung $\langle\cdot,\cdot\rangle:V\times W\to\mathbb{K}$ bilinear bzw. eine Bilinearform, wenn die Abbildungen $\langle \cdot, w\rangle:V\to\mathbb{K}$ und $\langle v,\cdot\rangle:W\to\mathbb{K}$ beide linear sind (d.h. wenn man eins der beiden Argumente festhält, ist die resultierende Abbildung linear), also wenn gilt:

$\langle v_1 + v_2, w\rangle = \langle v_1,w\rangle + \langle v_2,w\rangle$ und $\langle \lambda v, w\rangle = \lambda\langle v,w\rangle$
$\langle v,w_1 + w_2\rangle = \langle v,w_1\rangle + \langle v,w_2\rangle$ und $\langle v, \lambda w\rangle = \lambda\langle v,w\rangle$

Zum Beispiel ist das Skalarprodukt eines Vektorraums eine Bilinearform (die zusätzlich symmetrisch und positiv definit ist).

Die Matrixdarstellung einer Bilinearform $\beta$ bezüglich einer Basis $\mathcal{B}=(v_1,\ldots,v_n)$ ist: $$M_\mathcal{B}(\beta)=(\beta(v_i,v_j))$$ Die Matrixdarstellungen bezüglich verschiedener Basen sind immer kongruent.

Eine Bilinearform ist genau dann symmetrisch, wenn ihre Matrixdarstellung symmetrisch ist.

Eine Bilinearform ist alternierend, falls $\langle v,v \rangle = 0$ für alle $v\in V$ .

Eine Bilinearform ist schiefsymmetrisch, falls $\langle v,w \rangle = - \langle w,v\rangle$ .

Diese Begriffe sind meist äquivalent: Jede alternierende Bilinearform ist schiefsymmetrisch. Und umgekehrt auch, wenn $1+1\neq 0$ in $\mathbb{K}$ .

Eine Bilinearform ist nicht ausgeartet, wenn gilt:

Ist $\langle v,w\rangle = 0$ für ein festes $v$ und jedes $w$ , so ist $v=0$ .
Ist $\langle v,w\rangle = 0$ für jedes $v$ und ein festes $w$ , so ist $w=0$ .

Das ist genau dann der Fall, wenn ihre Matrixdarstellung den größtmöglichen Rang hat.

Endomorphismen auf Euklidischen Vektorräumen

Zu jedem Endomorphismus $f$ gibt es genau einen adjungierten Endomorphismus $f^\text{ad}$ , so dass $\langle v,f(w)\rangle = \langle f^\text{ad}(v), w\rangle$ für alle Vektoren $v,w$ des Vektorraums.

Ein Endomorphismus $f$ ist selbstadjungiert, wenn $f=f^\text{ad}$ , d.h. wenn $\langle v, f(w)\rangle = \langle f(v),w\rangle$ für alle Vektoren $v,w$ .

Im kanonischen Euklidischen Vektorraum ist die Matrixdarstellung des adjungierten Endomorphismus die transponierte Matrixdarstellung des Endomorphismus: $M_\mathcal{B}(f^\text{ad}) = (M_\mathcal{B}(f))^T$ .

Für $f(v) = Av$ ist $f^\text{ad}(v) = A^Tv$ .
Die Matrixdarstellung eines selbstadjungierten Endomorphismus ist diagonalisierbar.