Fluids comprise both liquids (generally incompressible, i.e. volume does not change in response to a pressure change) and gases (compressible).

Steady flow

Flow rate: \(\Phi_V = \cfrac{\Phi_m}{\rho}\) .

Velocity: \(v = \cfrac{\Phi_V}{A}\) With \(A\) the cross-sectional area.

The flow rate has an impact on whether the flow is laminar (usually at low velocities), turbulant (usually at high velocities) or in some transition phase between the two types.

• Laminar flow is ordered, characterized by smooth layers of fluid. Viscous forces dominate.
• Turbulant flow is disordered. Inertial forces dominate.

Continuity states that for an incompressible fluid flowing in a pipe, the flow rate is the same everywhere in the pipe: $$\rho_1 A_1 v_1 = \rho_2 A_2 v_2$$ With \(\rho\) the density, \(A\) the cross-sectional area, and \(v\) the velocity.

Drag force

A solid object moving through a fluid generates a drag force.

(Image source: 7700.com)

Friction drag mainly depends on the surface area parallel to the flow.

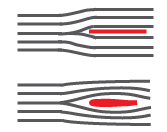
Form drag mainly depends on the surface area perpendicular to the flow. It creates a pressure difference, due to an agglomeration of fluid in front of the object and a corresponding lack of fluid behind it.

The drag force is determined as follows: $$F_D = C_D\cdot A\cdot \frac{1}{2}\rho_f v_r^2$$ Where:

• \(A\) is the relevant cross-sectional area of the object. This is \(A_\bot\) for form drag (the area perpendicular to the flow).
• \(v_r\) is the relative velocity of object and fluid: \(v_r = v_f - v_o\)
• \(\rho_f\) is the density of the fluid.
• \(C_D\) is the object’s drag coefficient.

The drag coefficient is a function of the object’s shape and the Reynolds number: $$Re = \cfrac{\rho_f v_r D}{\mu}$$ Where \(\mu\) the viscosity of the fluid and \(D\) the diameter of the object. The Reynolds number describes the ratio of inertial forces to viscous forces in a flowing fluid.

Finding an analytical solution for the drag coefficient from the flow equations is possible only for low Reynolds number (< 1) and simple shapes. In the case of spheres, the drag coefficient is \(C_D=\frac{24}{Re}\) , which yields a drag force following Stoke’s law: $$F_D = 3\pi D \mu v_r$$ Where form drag contributes \(\pi\mu Dv\) and friction drag contributes \(2\pi\mu Dv\) . (Note that the viscosity \(\mu\) of the fluid is important, not its density.)

For large Reynolds numbers (> \(10^4\) ), \(C_D\) is constant.

For flows with a low Reynolds number, most drag is due to friction. These are laminal flows. For flows with a high Reynolds number, form drag increases due to the pressure difference becoming significant. These are turbulent flows.

Determining the drag coefficient iteratively

Start with a rough estimate for the drag coefficient. For a high Reynolds number, for example, we can start assuming \(C_D=1\) .

1. Compute according velocity \(v\) .
2. Based on the velocity, compute the Reynolds number \(Re=\cfrac{\rho_\text{fluid} v D}{\mu_\text{fluid}}\) .
3. Look up the drag coefficient \(C_D\) for that Reynolds number (given the object’s shape).

Iterate until \(C_D\) and \(v\) don’t change anymore.

Terminal velocity

When an object is freely falling or rising through a fluid, as its velocity increases, so does the drag restraining the movement. At some point, these forces are balanced, and since there is no net force on the object, its acceleration is zero. It is then falling or rising with its terminal velocity, the steady-state velocity of an object in a fluid when its acceleration is zero and all upward and downward forces are balanced.

For falling objects: \(F_\text{gravitation}=F_\text{buoyancy} + F_\text{drag}\)

For rising objects: \(F_\text{buoyancy} = F_\text{gravitation} + F_\text{drag}\)

Where:

• \(F_\text{gravitation}=mg=\rho_\text{object} V g\)
• \(F_\text{buoyancy}=mg=\rho_\text{fluid} V g\)
• \(F_\text{drag}=C_D A \frac{1}{2}\rho_f v_t^2\) (see above)

Terminal velocity is the highest velocity the object can achieve falling freely through the fluid.